量子真随机数
随机性是一个非常有趣的概念,引起了大量学者的研究兴趣。从理论研究的意义上看,其属于物理学甚至是哲学的范畴,即研究世界的确定性问题:世界是确定性的,还是随机的呢?除了理论研究的意义外,随机性在实际应用中也是一种极其重要的资源,在很多领域中都发挥着重要的作用,如密码学、博弈、数值计算和生物系统的仿真等等。
通俗地讲,随机数序列是对一个均匀分布随机变量的一组抽样,其结果是不可预测的,序列中的每个数都是独立的,且服从均匀分布。随机数在密码学中应用非常广泛。在经典密码体制中,DES加密算法中的密钥、RSA加密算法中的素数及其密钥的产生都需要随机数。在《应用密码学》(吴世忠等著)所描述的众多密码学协议中,大多数都需用到随机数。而在量子密码方案中,参与者经常需要根据随机数来随机执行几种操作之一,或随机选择不同位置的测量结果用于检测窃听。显然,如果用户产生的随机数不够随机,攻击者知道这些数字的部分或全部信息,密码体制的安全性将受到严重威胁。
迄今为止,研究人员提出了许多不同的随机数生成方法。我们将这些方法所产生的随机数分为以下三种:表面随机数、真随机数和自验证真随机数,下面依次进行介绍。
一、表面随机数
提起随机数的产生方法,很容易联想到序列密码中的密钥流生成算法和日常生活中的抛硬币(如图1)。前者通过确定的函数作用在初始种子密钥上来获得密钥流,所产生的是“伪随机数”。相比之下,人们通常认为后者所产生的更像是真正的随机数。
事实上,任何基于经典过程(即经典力学的过程)所产生的随机数本质上都不是真随机的,因为经典系统中的随机性都是“表面随机性”。所谓表面随机性,故名思议就是事件表面上看似具有随机性,而本质上并不是随机的,只是确定性事件的概率组合。它之所以表现出随机性,是因为观察者对系统整体运作机制的不完全了解。由表面随机性所产生的随机数并不是真正随机的,这里称之为“表面随机数”。
图1 抛硬币游戏
下面以经典抛硬币游戏为例说明为何它产生的随机数不是真随机的。当我们抛掷一枚硬币时,从力学的角度看,硬币落地的正反面结果其实是一个确定性的事件。一旦我们明确知道硬币抛出时的角度、速度、在空气中受到的风力、阻力及落地时地面的粗糙程度等所有外在影响因素,那么其落地的正反面结果完全可以根据力学规律推导出来,是确定的,而不再是随机的。试想一下,如果假设每次抛硬币的外在因素都是完全一样的,那么得到的结果会如何呢?显然一定会是相同的结果,而不会是随机的。当然这一假设并不容易实现,而外在因素稍有差异就可能会引起结果的不同,所以我们每次抛硬币的结果看起来就像是随机的了。
由此可见,抛硬币不能产生真正的随机数。而基于其它经典物理过程(如掷骰子、转轮、电子元件的噪音等)所产生的随机数也是如此。那么,我们有没有可能产生真正的随机数呢?随着量子力学的发展,人们在量子系统中找到了肯定的答案。
二、真随机数
“量子”是一个不可分割的基本个体,是构成现实事物的微小能量和物质,如光子、原子、电子都是“量子”的组成微粒。量子力学是研究微观世界力学规律的理论,其正确性已经逐步得到证实。研究表明,微观粒子的状态具有“内禀随机性”。也就是说,其随机性不是因为缺乏对系统的了解而造成的,而是微观粒子固有的特性。利用这种内禀随机性,可以产生真正的随机数,即“真随机数”(或称为“内禀随机数”)。
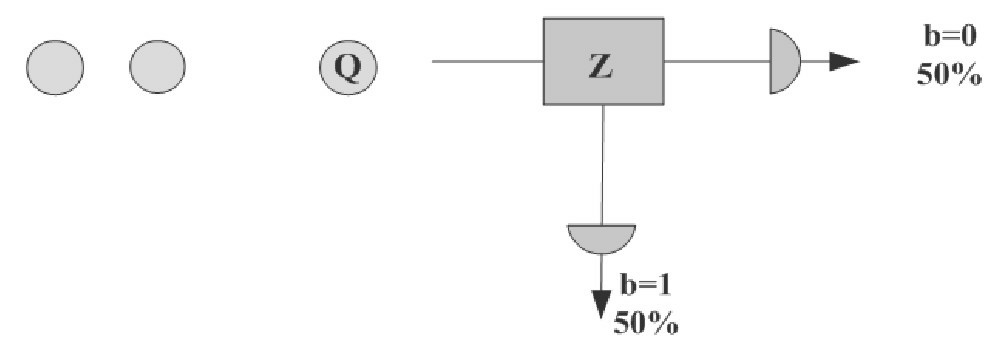
图2 量子态的测量
下面以量子比特的测量为例介绍量子系统中的内禀随机性。如图2,考虑处于叠加状态的量子比特Q:|φ〉=(1/)(|0〉+|1)(其中|〉为量子状态的Dirac表示,|0〉,|1〉为两个基矢态)。当使用{|0〉,|1〉}基(即Z基)测量该量子比特时,将以1/2的概率测得|0〉,1/2的概率测得|1〉。如果用b=0,1分别对应这两种结果,则b就是产生的随机比特。值得注意的是,量子态的测量与抛硬币情况不同,这里出现的随机性是量子系统所固有的,而不是因为对系统的不了解而产生的。也就是说,用这样的测量方式来观测这样的态(两者均明确已知),其观测结果就是随机的,这是由量子力学基本原理决定的。
再举一个更容易理解的例子。分束器是常用的光学实验器件,可以理解为是一块薄片状的晶体。一个透、反射比为1∶1的分束器会把入射光平均分成两半,一半透射过去,一半反射出去。但当只有一个光子(即一个量子,不可再分)入射时,它会以1/2的概率透射,1/2的概率反射。这是光子和分束器的本质属性决定的。如果观测到透射和反射分别记为0和1,则据此可获得随机数。
上述利用量子系统的内禀随机性产生的随机数就是真随机数。然而,量子力学的神奇之处还不止如此。实际上随机数包括两方面的要求:一是“等概性”,即每个比特0和1出现的概率相等;二是“独立性”,即每个比特与其它任何变量(包括该随机数中的其它比特和外部变量)都统计独立。上面讨论中,我们只考虑了“等概性”。下面我们讨论“独立性”。前文提到,随机数的安全性对密码系统的安全性至关重要。一旦攻击者知道了用户在密码算法中所使用的随机数,很多密码系统的安全性将完全崩溃。考虑这样一种情形,我们产生随机数的设备(可以想象成一个内部不断抛硬币或观测单光子透、反射并输出结果的盒子,具体使用时用户看不到其内部工作过程,只能看到输出结果)是购买而来的,供应商在制造设备时可能采取了某些策略按自己的利益影响着它的输出结果,甚至是事先预设一些(看起来随机的)比特串存储在设备中,使得输出的序列对于供应商来说是部分已知的甚至是完全已知的,即输出结果不满足“独立性”。因此,密码系统中必须要保证所产生的随机数与其它外部变量完全无关,即包括设备供应商在内的其他任何人都不能获知该随机数的任何信息。这一点在经典世界中是难以实现甚至无法想象的。然而随着设备无关量子密码的发展,人们提出了设备无关量子随机数扩展方法。该方法可以保证所产生的真随机数与外部变量无关,因此我们称之为“自验证真随机数”(本文中的“验证”均指验证所产生的随机数与外部变量无关)。
三、自验证真随机数
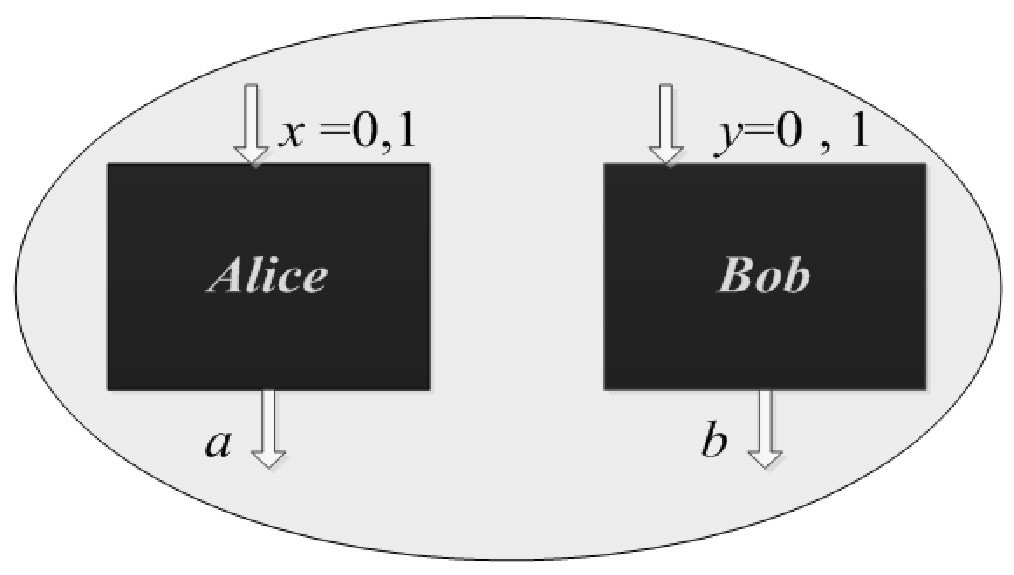
图3 设备无关量子随机数扩展
设备无关量子随机数扩展,最早由RogerColbeck在2007年提出,之后引起了众多学者的研究兴趣。为了实现可验证的目的,该方法需要一些随机数作为种子,进而产生新的随机数,因此被称为随机数“扩展”。需要强调的是,量子随机数扩展产生的新随机数与原来的随机数种子之间没有任何关系,因此种子和新随机数都可以作为输出使用。
设备无关量子随机数扩展的主要思想是把产生设备看成黑盒子,不对设备内部的参数做任何假设(这样就可以免疫所有设备不完美或不可信因素)。设备以随机数种子作为输入,接收到输入后设备相应地输出经典比特,之后统计输入输出之间的关联关系。如果此关系超出了经典物理范畴,那么它就是一种量子关联关系,此时设备中必含有量子系统,并且至少部分地在按照说明书中所描述的正确方式在工作。根据这种关联关系的具体数值,用户可以从输出结果中提取相应数量的自验证(与外部变量无关的)真随机数。2010年,StefanoPironio等在Nature主刊上首次给出了基于CHSH-Bell不等式的设备无关量子随机数扩展的实验,并计算出生成序列中所包含的真随机数的量。下面我们对其进行简单的描述。
实验装置可以简化为图3所示,椭圆区域表示一个安全实验室:它不会主动向外泄露信息,且攻击者也无法进入该区域。装置中的两个黑盒子用于产生随机数,记为Alice和Bob。x,y分别为Alice和Bob的输入,a,b分别为Alice和Bob的输出。Alice和Bob各有两个测量力学量,且每个测量力学量都对应两个输出结果,用0或1表示。连续进行多次实验,每一次实验Alice和Bob都根据随机数种子x,y随机独立地选择测量力学量,且两个测量同时进行(或者更准确地说,两个黑盒类空间隔),然后统计概率分布,并计算以下概率分布的线性组合:
![]()
在任何局域实在性理论中该组合所能达到的最大值均为2,因此任何经典事件都不会违背该值。但在量子理论中CHSH却能违背此值,其最大值可以达到2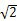 。这就是著名的CHSH-Bell不等式。所以在实验中我们只需要统计CHSH的值,一旦其值大于2,我们可以断定设备中必定含有量子系统,并且至少部分地在按照说明书中所描述的正确方式工作,用户可以从输出结果中提取相应数量的自验证真随机数。在理想情况下(实验进行无数次,统计得到的频率无限接近概率,并且每次实验之间没有相互影响)所产生真随机性的量与CHSH的值之间的关系为:H∞(a,b|x,y)≥f(CHSH)。其中真随机性的量用条件极小熵H∞(a,b|x,y)刻画,f是如图4所示的凸函数。若条件极小熵H∞=0,说明输出结果(a,b)中没有真随机性;若H∞=2,说明(a,b)全部是真随机的;而当H∞=m(0<m<2)时,说明(a,b)中有m比特的真随机性,进而可以利用随机数提取算法提取出m长的自验证真随机数。
。这就是著名的CHSH-Bell不等式。所以在实验中我们只需要统计CHSH的值,一旦其值大于2,我们可以断定设备中必定含有量子系统,并且至少部分地在按照说明书中所描述的正确方式工作,用户可以从输出结果中提取相应数量的自验证真随机数。在理想情况下(实验进行无数次,统计得到的频率无限接近概率,并且每次实验之间没有相互影响)所产生真随机性的量与CHSH的值之间的关系为:H∞(a,b|x,y)≥f(CHSH)。其中真随机性的量用条件极小熵H∞(a,b|x,y)刻画,f是如图4所示的凸函数。若条件极小熵H∞=0,说明输出结果(a,b)中没有真随机性;若H∞=2,说明(a,b)全部是真随机的;而当H∞=m(0<m<2)时,说明(a,b)中有m比特的真随机性,进而可以利用随机数提取算法提取出m长的自验证真随机数。
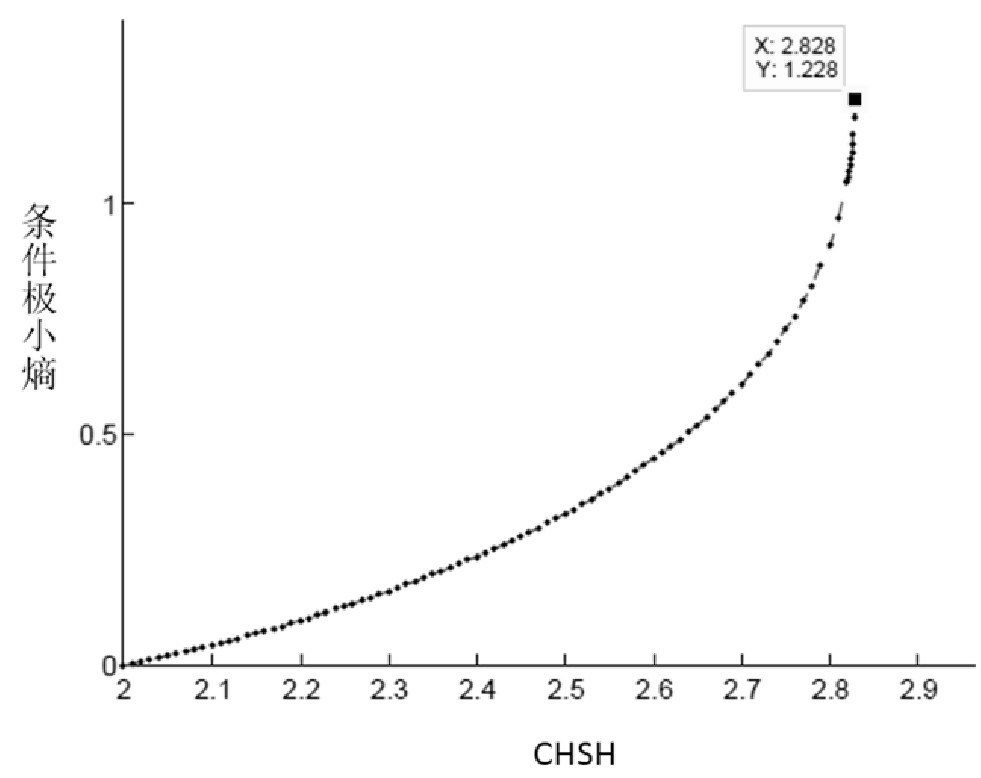
图4 获得的真随机性与CHSH值之间的关系
综上,量子力学原理可以保证一旦违背发生,获得的随机性就是内禀的,且与任何其他变量无关的,进而可以提取出自验证真随机数。除了基于上述CHSH-Bell不等式的设备无关量子随机数扩展外,目前学者们也提出了基于GHZ悖论、Mermin不等式、KS不等式、链式Bell不等式及量子目击违背等同类方案。此外,最初的方案要求所使用的随机数种子是完全独立于其它变量的。后来EnshanKoh等和RogerColbeck等指出,只要独立程度高于一定的阈值,用与其它变量有关联的随机数种子也能产生新的自验证真随机数。能否充分发掘量子力学特性,设计出各类性能指标更优的扩展方案,是目前学者们正在研究的方向。
经典世界中的随机性是表面随机性,因而不能产生真随机数。而量子世界特有的性质确保了其不同于经典世界,具有内禀随机性,因此可以产生真正的随机数。除此之外,设备无关量子随机数扩展方案还可以实现随机数的扩展,同时保证扩展出的新随机数是可信的(即与任何外部变量都没有关联)。使用这种方案时,即使用户不信任设备供应商,也可以确保其它任何人都不知道自己所产生的随机数的任何信息,因此具有重大的理论意义和实际价值。(王玉坤、高飞、秦素娟、温巧燕)




 京公网安备11040102700137号
京公网安备11040102700137号
